Rolling without Slipping
Rolling without Slipping: Overview
This topic covers concepts, such as, Rolling Motion of a Rigid Body, Pure and Impure Rolling Motion, Accelerated Pure Rolling on Rough Inclined Ground & Role of Friction in Accelerated Pure Rolling etc.
Important Questions on Rolling without Slipping
At time , a disk of radius starts to roll without slipping on a horizontal plane with an angular acceleration of . A small stone is stuck to the disk. At , it is at the contact point of the disk and the plane. Later, at time , the stone detaches itself and flies off tangentially from the disk. The maximum height (in ) reached by the stone measured from the plane is . The value of is [Take .]
If the numerical value has more than two decimal places, truncate/round-off the value to TWO decimal places.
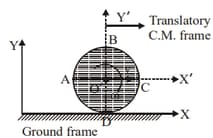
A thin rigid uniform circular disc rolls without slipping on a horizontal rigid surface (or the ground). At a certain instant, its position w.r.t. ground frame is as shown in the figure.
The diagram shows a uniform smooth solid cylinder of radius rolling without slipping on the plank, which in turn is supported by a fixed smooth surface. The blocks and both accelerates down with and respectively. The angular acceleration of the cylinder is , the acceleration of centre of mass of cylinder is , the ratio of mass of cylinder to the mass of block is . The length of the unwrapped thread between the cylinder and the block at is and at is (assume the system to be released from rest), match the following,
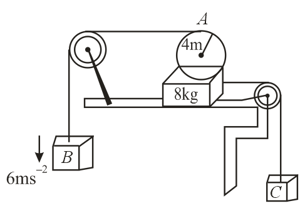
| COLUMN-I | COLUMN-II | ||
| A) | in | p) | |
| B) | q) | ||
| C) | r) | ||
| C) | s) |
A uniform ting placed on a rough horizontal surface is given a sharp impulse as shown in the figure. As a consequence, it acquires a linear velocity of If coefficient of friction between the ring and the horizontal surface is
Consider a sphere of mass radius in pure rolling on a rough horizontal surface having velocity as shown in the figure. It makes an elastic impact with a smooth vertical wall and moves back and starts pure rolling after some time again. Now
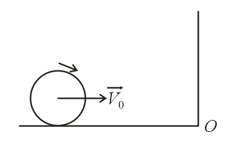
A small disc of mass is released on a parabolic curve in a vertical plane such that gravity acts along negative -axis. The equation of parabolic curve is where ' is a positive constant. Frictional force between disc and curve are sufficient for pure rolling. When disc is reached at then choose the correct option(s).
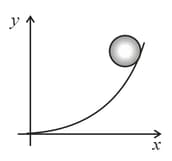
The angular velocity and the angular acceleration are plotted with time as shown. Which of the following options are incorrect?
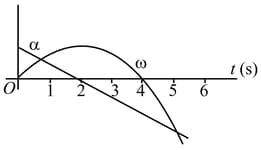
A half section of pipe of mass and radius rests on a rough horizontal surface. Now a vertical force is applied as shown. Assuming that the section rolls without sliding. Then [Centre of mass of half ring is below the centre]
The figure shows a plank of mass kept on a smooth inclined plane of inclination with the horizontal. A man(mass ) starts running on the rough surface of the plank such that plank remains stationary w.r.t ground. Choose the incorrect option(s)
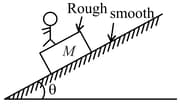
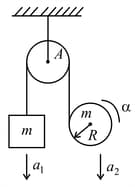
An ideal inextensible string is wrapped over the disc of mass and radius . The other end of the string is connected to mass . The string is passing over an ideal pulley as shown in the figure. At any time , mass and disc are moving downward with acceleration of magnitudes and respectively. The disc is rotating clockwise with angular acceleration of magnitude . There is no slipping between string and disc. Choose the INCORRECT option.
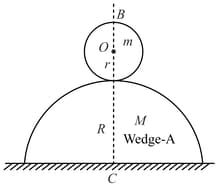
A semi-Cylindrical wedge of mass and radius is placed on a horizontal smooth surface. A solid cylinder of mass and radius is placed at the top of the wedge as shown in the figure, and released with a gentle rightward push. There is no friction between the curved surface of semi cylinder and solid cylinder. Find the velocity of the wedge when the line makes an angle of with the vertical. (given and )
A cylindrical shell, a spherical shell and a solid sphere are allowed to roll on an inclined rough surface of co-efficient of friction and inclination The correct statements are
A wheel of radius rolls without slipping with a speed over a horizontal road. When it is at a point on the road; a small lump of mud separates from the wheel at its highest point and lands on the road at a point . Then
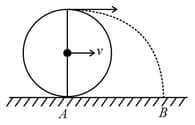
A uniform disc is performing pure rolling on a smooth horizontal stationary surface with constant angular velocity () and linear velocity of centre of mass as shown is fig. find the correct statements at the given instant of time (Radius of the disc is ) (Assume are on the circumference of the disc.)
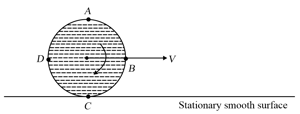
A disc of radius rolls on a horizontal surface with linear velocity and angular velocity . There is a point on circumference of disc at angle with upward vertical diameter measured anticlockwise see figure, which has a vertical velocity. Here is equal to
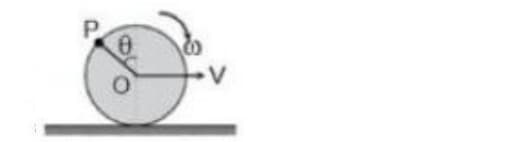
The minimum force required to roll a rigid sphere up a vertical wall is (The coefficient of friction between sphere and the wall is )
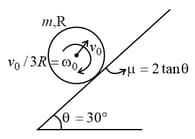
A solid sphere of mass and radius is projected up an inclined plane of inclination with an initial velocity and initial angular velocity as shown. The coefficient of friction between the sphere and inclined plane is . Then find the velocity (in ) of the sphere, when it will rolling without slipping relative to the inclined plane.
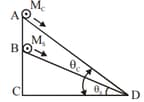
A cylinder of mass and sphere of mass are placed at points and of two inclines, respectively. (See Figure). If they roll on the incline without slipping such that their accelerations are the same, then the ratio . What is the value of ?
A uniform solid ball of mass '' rolls without sliding on a fixed horizontal surface. The velocity of the lowest point of the ball with respect to the center of the ball is . The total kinetic energy of the ball is:
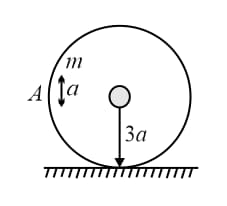
A ring of radius is fixed rigidly on a table. A small ring whose mass is and radius rolls without slipping inside it as shown in the figure. The small ring is released from position . When it reaches the lowest point, the speed of the centre of the ring at that time would be,